
Deep Learning: Foundation & Concepts - Chapter 4

单层网络:回归 (Regression)
Summary by Chandery | Chapter 4 in Deep Learning: Foundation and Concepts | 2025年10月
在本章中,我们使用线性回归框架讨论了神经网络背后的一些基本思想,这能简要地帮助我们了解多项式曲线拟合。我们将看到,线性回归模型对应于具有单层可学习参数的简单形式的神经网络。尽管单层网络的实际应用非常有限,但它们具有简单的分析性质,并为引入许多核心概念提供了一个很好的框架,这些概念将为我们在后面的章节中讨论深度神经网络奠定基础。
线形回归
回归的目的是在给定
最简单的回归模型的形式被表示为对输入变量的线性组合:
其中
线性回归这一术语有时特指这种形式的模型。该模型的关键特性是它是参数
注意: 这里是因为由于对于输入变量是线性的,模型不管怎么叠加,都存在一种一层的线性变换与之等价。模型无法表达非线性的分布。
基函数
我们可以把先前简单的模型形式扩展为使用非线性函数对输入变量
其中
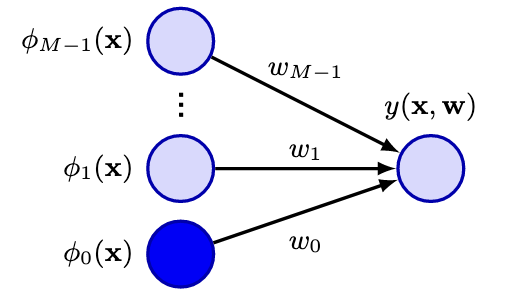
这里,每个基函数
使用了基于非线性的函数后,
在深度学习出现之前,机器学习的时间中通常对输入变量\textbf{x}进行一些形式的预处理——通常被称为特征提取(feature extraction)——用一组基函数表示{
在第一章中简要提到的线性模型的形式为:
这里的
这里的
注意: 归一化系数指的是高斯分布前面的
或者用sigmoid(> 注意: S型的)基函数
同样我们也可以用tanh函数因为它的表达式

左边展示基于多项式的基函数;中间展示高斯基函数;右边展示Sigmoidal(S型)基函数
似然函数
我们使用最小化平方损失函数的方法来你和多项式函数,在一种高斯噪声模型的假定下,这种误差函数可以作为最大似然解。
推导说明:
这里对这句话进行一个推导:
我们考察一个假设:对于观测值
,我们认为它是某个真实函数的输出加上高斯噪声。假设有一个模型预测值 ,其中 是我们要拟合的函数, 是模型参数。 模型设定:
我们假设观测值可以表示为:
其中是一个高斯噪声,满足 。 似然函数:
因此,在给定参数的条件下,观测值 的概率密度可以表达为: 对数似然函数:
对上述似然函数取对数,得到对数似然函数:最大化对数似然:
为了执行最大似然估计,我们需要最大化对数似然函数。由于是一个常数,不依赖于 ,因此最大化对数似然函数相当于最大化项: 最大化这个表达式意味着最小化平方项,即:
因此,从这里我们得出最小化平方损失函数与最大化似然函数是等价的。
同样的,我们假设目标变量
这里
然后我们考虑输入的集合
对这个似然函数取对数
$$\ln p(\textbf{t}|X, \textbf{w},\sigma^2) = \sum_{n=1}^{N}\ln\mathcal{N}(t_n|\textbf{w}^T\phi(\textbf{x}n),\sigma^2)=-\frac{N}{2}\ln\sigma^2-\frac{N}{2}\ln(2\pi)-\frac{1}{2\sigma^2}\sum{n=1}^{N}{t_n-\textbf{w}^T\boldsymbol{\phi}(\textbf{x}_n)}^2 \quad (11)$$
极大似然
写完似然函数之后我们使用极大似然来得到\textbf{w}和
令该梯度为零得
$$0=\sum_{n=1}^{N}t_n\boldsymbol{\phi}(\textbf{x}n)^T-\textbf{w}^T\left(\sum{n=1}^{N}\boldsymbol{\phi}(\textbf{x}_n)\boldsymbol{\phi}(\textbf{x}_n)^T\right) \quad (13)$$
化简得到\textbf{w}的值为
这个被称为最小二乘法问题的正规方程。这里的
$$\boldsymbol{\Phi}=\left(\begin{array}{cccc}\phi_0(\mathbf{x}_1) & \phi_1(\mathbf{x}1) & \cdots & \phi{M-1}(\mathbf{x}_1) \phi_0(\mathbf{x}_2) & \phi_1(\mathbf{x}2) & \cdots & \phi{M-1}(\mathbf{x}_2) \vdots & \vdots & \ddots & \vdots \phi_0(\mathbf{x}_N) & \phi_1(\mathbf{x}N) & \cdots & \phi{M-1}(\mathbf{x}_N)\end{array}\right) \quad (15)$$
式子
被称为矩阵
此时我们可以对偏置参数
令该式对
其中我们定义
可以看到偏差
同样的,我们可以对取对数后的似然函数对方差
因此,我们看到方差参数的最大似然值由回归函数周围目标值的残差方差给出。
最小二乘法的几何意义
我们考虑一个N维空间的轴由
在实际应用中,如果
注意: 这点在后面的 1.6正则化最小二乘会详细阐述
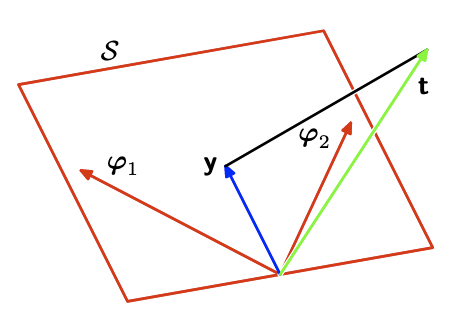
最小二乘法的几何解释
顺序学习
极大似然估计的方法设计一次性处理整个训练集,被称为批处理方法。这种方法对于发数据集来说计算成本变得很高。如果使用顺序算法(也被称为在线算法)可能是更好的。在这种算法中,依次考虑一个数据点,并在每次实施后更新模型参数。
我们可以通过一个叫随机梯度下降也叫顺序梯度下降的技巧来实现顺序学习算法。具体的,如果误差函数被表示为和的形式如
其中
其中
正则化最小二乘
我们先前介绍了在误差函数中天机啊正则项来控制过拟合的想法,因此总的误差函数的形式为
其中
如果我们考虑均方误差函数
那么总的误差函数就变成
在统计学中,这个正则化提供了参数收缩方法的一种示例,因为它将参数值收缩到零。他的优点是误差函数仍是\textbf{w}的二次函数,因此它的精确最小值可以以闭合形式找到。具体来说,将式(26)对\textbf{w}的梯度设为零,并且求解\textbf{w},得到
这提供了一个最小二乘法(式14)的简单的扩展。
多输出
目前,我们已经考虑了只有一个目标变量
其中
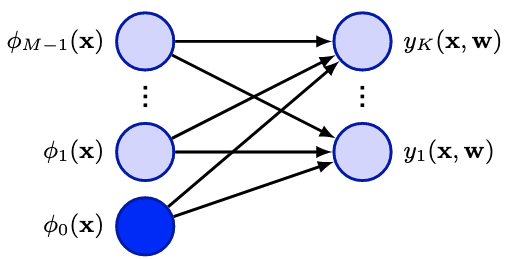
类似图4.1,输出端换成了多输出
考虑使目标向量的条件分布写成一个高斯各向同性的形式(> 注意: 每个方向的协方差都相等,没有偏好)
如果我们有一组观测值
$$\begin{aligned}\ln p(\mathbf{T}|\mathbf{X},\mathbf{W},\sigma^2) & =\sum_{n=1}^N\ln\mathcal{N}(\mathbf{t}_n|\mathbf{W}^\mathrm{T}\boldsymbol{\phi}(\mathbf{x}n),\sigma^2\mathbf{I}) \& =-\frac{NK}{2}\ln\left(2\pi\sigma^2\right)-\frac{1}{2\sigma^2}\sum{n=1}^N\left|\mathbf{t}_n-\mathbf{W}^\mathrm{T}\boldsymbol{\phi}(\mathbf{x}_n)\right|^2.\end{aligned} \quad (30)$$
和之前一样,我们对\textbf{W}求导,令它为零,得到
其中我们把输入特征向量
其中 $\textbf{t}k
对具有任意协方差矩阵的一般高斯噪声分布的扩展是直接的。同样,这导致了与K无关的回归问题的解耦。这一结果并不令人惊讶,因为参数\textbf{W}仅定义了高斯噪声分布的均值,我们知道多元高斯均值的最大似然解与其协方差无关。因此,从现在开始,为了简单起见,我们将考虑单个目标变量t。
决策理论
先前,我们把回归任务转化为了建立一个条件概率分布
$$p(t|\textbf{x},\textbf{w}{ML},\sigma^2{ML})=\mathcal{N}(t|y(\textbf{x},\textbf{w}{ML}),\sigma^2{ML}) \quad (33)$$
这个预测分布表达了我们在重新输入一个新的\textbf{x}之后结果的\textbf{t}的不确定性。然而,在很多实际的应用中我们需要具体的值
- 推理阶段:我们经过推理得到预测的分布
- 决策阶段:我们使用得到的分布确定一个具体的值
我们可以使用最小化同时依赖于预测分布
直觉来说,我们会选择条件分布的均值,因此我们令
考虑我们在预测的时候选择一个值
其中,我们对输入变量和目标变量的分布进行平均,由它们的联合分布
注意: 值得注意的是,不要弄混均方损失函数和前面介绍的平方和误差函数。误差函数用来在训练中设置参数,从而确定条件概率分布
,而损失函数控制着如何使用条件分布来对于每一个\textbf{x}值确定具体的预测函数 。
我们的目标是选择一个
使用概率的和与积的法则,我们可以推到
它是以\textbf{x}为条件的
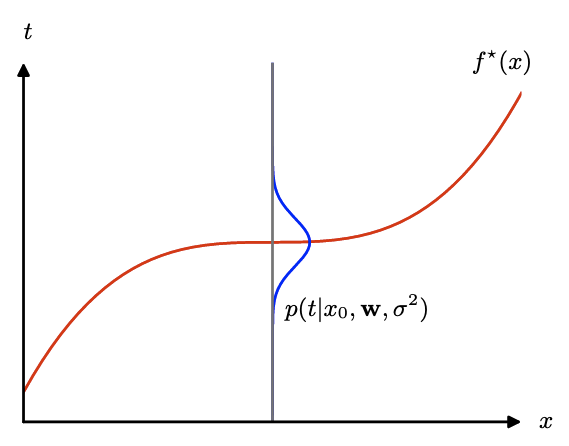
回归函数$f^(x)
结果如图4.5所示,并且很容易扩展到多输出的t,此时最优的条件均值解为
在式(37)中使用变分法进行推导意味着我们正在优化所有可能的函数
我们可以从一种不同的方式来推导这个问题,同样可以阐明回归问题的本质。首先明确优化问题本质上是一种条件期望,我们可以把平方项扩展为
其中为了符号简洁,我们使用
推导说明:
这里进行推导
交叉项
是因为,首先 不依赖 , 第三项
,
均方损失并不是这里的唯一选择,我们可以简单地考虑一种经过简单泛化的函数,被称为闵可夫斯基损失,其期望值由下式给出
图4.6展示了不同 q 的取值下
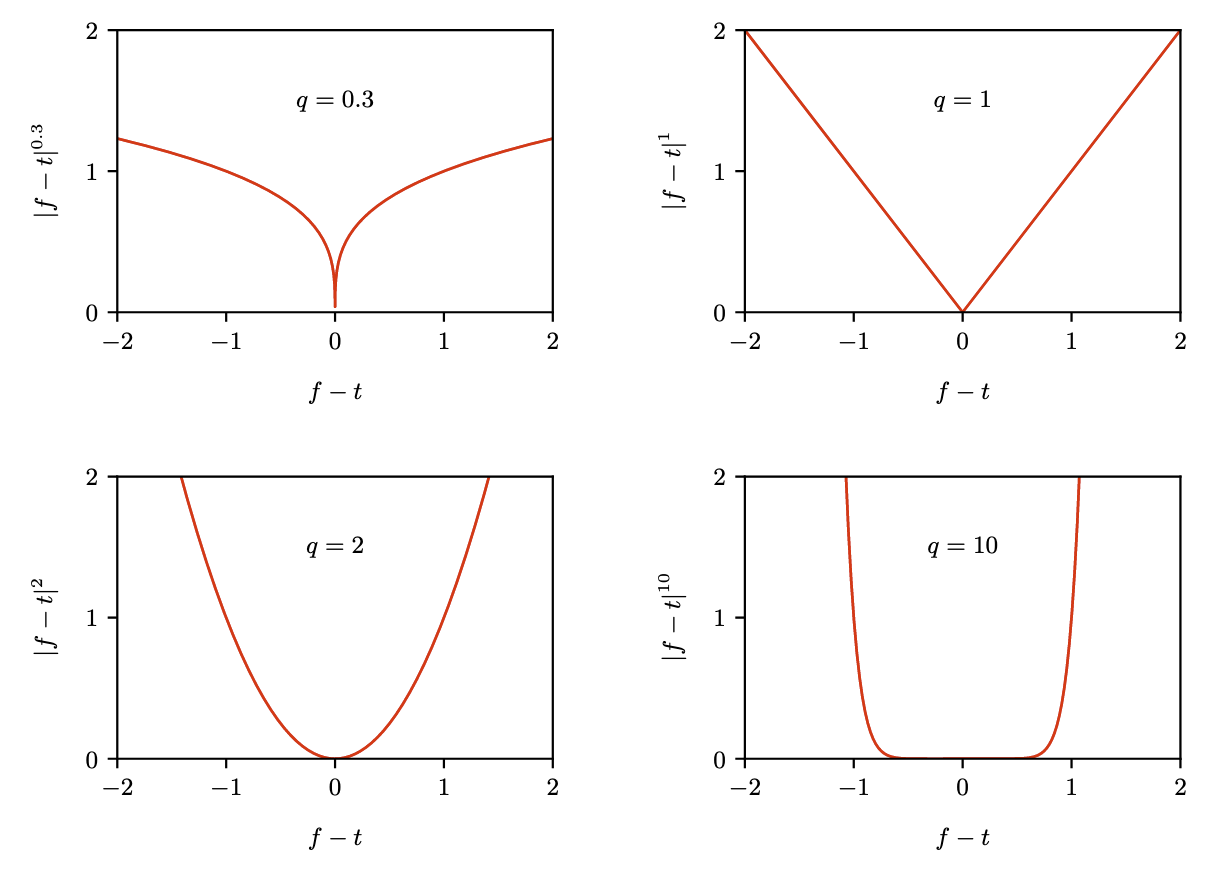
不同 q 的损失图像
偏差和方差的权衡
在线性模型中目前有几个问题:
- 太多的基函数会导致过拟合
- 如果限制基函数的数量又会导致欠拟合
- 虽然正则化可以一定程度控制过拟合,但是引出了如何选择系数
- 如果同时考虑权重向量\textbf{w}和正则化系数
这时候考虑模型复杂性问题中的频率论观点,即偏差-方差权衡。
在决策理论中我们使用了很多不同类型的损失函数,当我们引入条件分布
使用我们常用的平方损失得
其中第二项和
如果我们有无限的数据,无限的计算资源,理论上我们可以在任意的精度下找到回归函数
如果我们使用由参数向量\textbf{w}控制的函数对
对于式(43)中第一项的被积函数,我们加入特定的数据集
同样的我们对其进行类似式(39)的变形
$$\begin{gathered}{f(\mathbf{x};\mathcal{D})-\mathbb{E}_\mathcal{D}[f(\mathbf{x};\mathcal{D})]+\mathbb{E}_\mathcal{D}[f(\mathbf{x};\mathcal{D})]-h(\mathbf{x})}^2 \={f(\mathbf{x};\mathcal{D})-\mathbb{E}\mathcal{D}[f(\mathbf{x};\mathcal{D})]}^2+{\mathbb{E}\mathcal{D}[f(\mathbf{x};\mathcal{D})]-h(\mathbf{x} \+2{f(\mathbf{x};\mathcal{D})-\mathbb{E}{\mathcal{D}}[f(\mathbf{x};\mathcal{D})]}{\mathbb{E}{\mathcal{D}}[f(\mathbf{x};\mathcal{D})]-h(\mathbf{x})}.\end{gathered} \quad (4)$$
然后我们对它在给定数据集
$$\begin{aligned}& \mathbb{E}{\mathcal{D}}\left[{f(\mathbf{x};\mathcal{D})-h(\mathbf{x})}^2\right] \& ={\mathbb{E}{\mathcal{D}}[f(\mathbf{x};\mathcal{D})]-h(\mathbf{x})}^2+\mathbb{E}{\mathcal{D}}\left[{f(\mathbf{x};\mathcal{D})-\mathbb{E}{\mathcal{D}}[f(\mathbf{x};\mathcal{D})]}^2\right].\end{aligned} \quad (45)$$
该式分为两项
- 第一项
- 第二项$\mathbb{E}{\mathcal{D}}\left[{f(\mathbf{x};\mathcal{D})-\mathbb{E}{\mathcal{D}}[f(\mathbf{x};\mathcal{D})]}^2\right]$被称为方差,用来衡量每个数据集的结果和所有数据集平均预测之间的不同程度。
现在如果我们把上述过程代入到式(43)中可得期望平方损失为
其中
$$\mathrm{variance}=\int\mathbb{E}{\mathcal{D}}\left[{f(\mathbf{x};\mathcal{D})-\mathbb{E}{\mathcal{D}}[f(\mathbf{x};\mathcal{D})]}^2\right]p(\mathbf{x})\operatorname{d}\mathbf{x} \quad (48)$$
注意: 这里相当于把损失项的第一项拆开,对于有限的数据集进行考虑,得到偏差和方差;而 noise 就是我们刚提到的因为高斯噪声模型而得到的期望损失最小可实现值。
因此这个损失函数的优化可以被看作是偏差和方差的权衡。对于约束少的模型来说可以做到偏差很小,但是方差较大;对于约束较多的模型来说可以做到方差很小,但是偏差较大。
作者在这里做了个实验,对函数
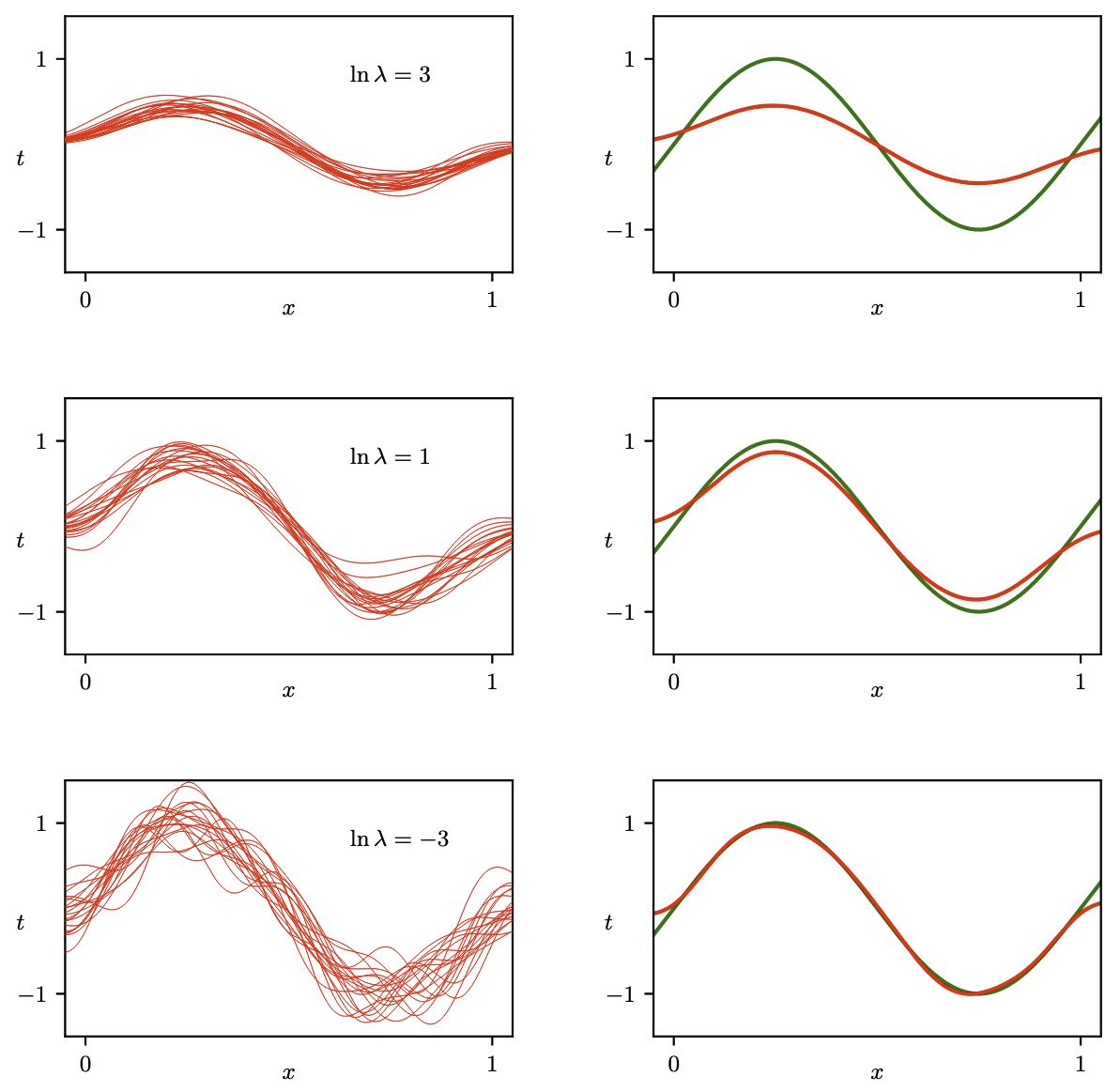
使用三种不同大小的
定量地,我们可以计算平均预测
偏差方和方差的积分式可以用离散均值的方式给出
图4.8展示了定量的结果对比。
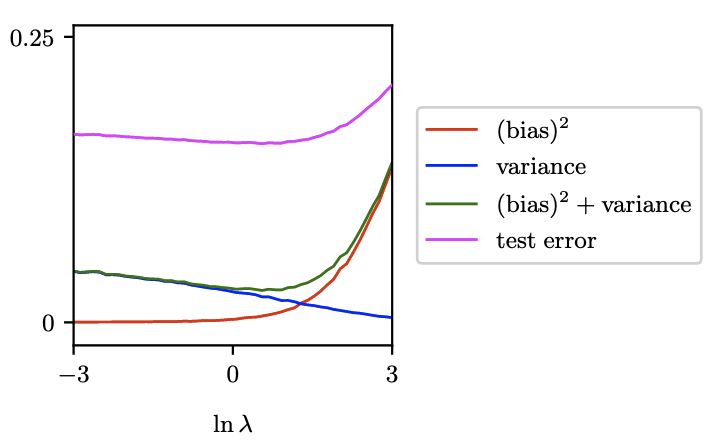 可以看到偏差方和方差的曲线趋势是相反的,这进一步印证了权衡。其中偏差方+方差的曲线的最小值和测试误差的最小值出现在相同点
可以看到偏差方和方差的曲线趋势是相反的,这进一步印证了权衡。其中偏差方+方差的曲线的最小值和测试误差的最小值出现在相同点
偏差-方差分解的实用价值有限,因为它基于数据集集合的平均值,而在实践中,我们只有一个观察到的数据集。如果我们有大量给定大小的独立训练集,我们最好将它们组合成一个更大的训练集,这当然会降低对给定模型复杂性的过度拟合程度。然而,偏差-方差分解经常为模型复杂性问题提供有用的见解,尽管我们在本章中从回归问题的角度介绍了它,但潜在的直觉具有广泛的适用性。
- Title: Deep Learning: Foundation & Concepts - Chapter 4
- Author: Chandery
- Created at : 2025-10-22 17:03:04
- Updated at : 2025-10-22 09:28:51
- Link: https://chandery.chat/2025/10/22/Deep-Learning-Foundation-Concepts-Chapter-4/
- License: This work is licensed under CC BY-NC-SA 4.0.